Matrices

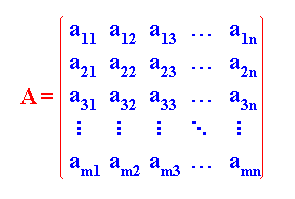
DEFINICIÓN DE MATRIZ: Se puede definir una matriz, como un conjunto de elementos (números) ordenados en filas y columnas.

 

IGUALDAD DE MATRICES: Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales

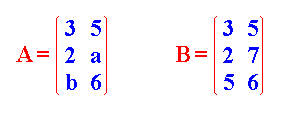
Para que las matrices  A  y  B  sean iguales, se tiene que cumplir que  a = 7  y  b = 5.

TIPOS DE MATRICES

Vamos a describir algunos tipos de matrices que aparecen con frecuencia debido a su utilidad, y de los que es conveniente recordar su nombre.

Matriz fila: Es una matriz que solo tiene una fila, es decir m =1 y por tanto es de orden 1xn.

Matriz columna: Es una matriz que solo tiene una columna, es decir, n =1 y por tanto es de orden m x1.

 

Matriz cuadrada: Es aquella que tiene el mismo número de filas que de columnas, es decir m = n. En estos casos se dice que la matriz cuadrada es de orden n, y no n x n.

Los elementos a_ij con i = j, o sea a_ii forman la llamada diagonal principal de la matriz cuadrada, y los elementos a_ij con i + j = n +1 la diagonal secundaria.

Matriz traspuesta: Dada una matriz A, se llama traspuesta de A, y se representa por A^t, a la matriz que se obtiene cambiando filas por columnas. La primera fila de A es la primera fila de A^t , la segunda fila de A es la segunda columna de A^t, etc.

 

Matriz simétrica: Una matriz simétrica es una matriz cuadrada que verifica:

                                   A = A^t.

Matriz antisimétrica: Una matriz antisimétrica o hemisimétrica es una matriz cuadrada que verifica:

A = -A^t.

Matriz nula: Es aquella que todos sus elementos son 0 y se representa por 0.

Matriz diagonal: Es una matriz cuadrada, en la que todos los elementos no pertenecientes a la diagonal principal son nulos.

Matriz escalar: Es una matriz diagonal con todos los elementos de la diagonal iguales.

Matriz unidad o identidad: Es una matriz escalar con los elementos de la diagonal principal iguales a 1.

Matriz Triangular: Es una matriz cuadrada que tiene nulos todos los elementos que están a un mismo lado de la diagonal principal. Las matrices triangulares pueden ser de dos tipos:

Triangular Superior: Si los elementos que están por debajo de la diagonal principal son todos nulos

Triangular Inferior: Si los elementos que están por encima de la diagonal principal son todos nulos.

SUMA Y DIFERENCIA DE MATRICES

La suma de dos matrices A=(a_ij), B=(b_ij) de la misma dimensión, es otra matriz S=(s_ij) de la misma dimensión que los sumandos y con término genérico s_ij=a_ij+b_ij. Por tanto, para poder sumar dos matrices estas han de tener la misma dimensión.

La suma de las matrices A y B se denota por A+B.

Propiedades de la suma de matrices:

1. A + (B + C) = (A + B) + C (propiedad asociativa)
2. A + B = B + A (propiedad conmutativa)
3. A + 0 = A (0 es la matriz nula)
4. La matriz –A, que se obtiene cambiando de signo todos los elementos de A, recibe el nombre de matriz opuesta de A, ya que A + (–A) = 0.

La diferencia de matrices A y B se representa por A–B, y se define como: A–B = A + (–B)

PRODUCTO DE UNA MATRIZ POR UN NÚMERO

El producto de una matriz A = (a_ij) por un número real k es otra matriz B = (b_ij) de la misma dimensión que A y tal que cada elemento b_ij de B se obtiene multiplicando a_ij por k, es decir, b_ij = k·a_ij.

El producto de la matriz A por el número real k se designa por k·A. Al número real k se le llama también escalar, y a este producto, producto de escalares por matrices.

Propiedades del producto de una matriz por un escalar

1. k (A + B) = k A + k B (propiedad distributiva 1ª)
2. (k + h)A = k A + h A (propiedad distributiva 2ª)
3. k [h A] = (k h) A (propiedad asociativa mixta)
4. 1·A = A (elemento unidad)

 

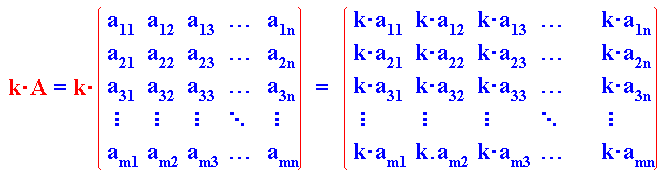
PRODUCTO DE MATRICES

El producto de matrices no está definido en todos los casos. Para que dos matrices se puedan multiplicar es necesario que el número de columnas de la primera matriz coincida con elnúmero de filas de la segunda matriz, es decir, si la matriz  A = ( a_ij )  tiene dimensión  m x n   y la matriz  B = ( b_ij )  tiene dimensión  p x q,  para que se pueda efectuar el producto A . B  es necesario que  n = p.  Por otra parte, la matriz producto  P = ( p_ij )  tendrá por dimensión  m x q, es decir, el número de filas de la matriz  A  y el número de columnas de la matriz  B. Cada elemento  p_ij  de la matriz  P  se obtiene multiplicando la fila  i  de la matriz  A  por la columna  j  de la matriz  B, siguiendo el procedimiento descrito en el punto anterior.

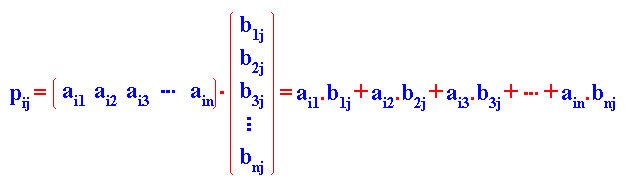
PROPIEDADES DEL PRODUCTO DE MATRICES:

Sean  A, B  Y  C  matrices. Siempre que sea posible efectuar los productos indicados, de acuerdo con la condición anterior, se verifica:

1ª  Asociativa:    ( A . B) . C = A . ( B . C )

2ª  Elemento neutro:   I   ( matriz identidad o unidad )       A . I = I . A = A

3ª  Distributiva respecto de la suma de matrices:   A . ( B + C ) = A . B + A . C

4ª  El producto de matrices no es, en general, conmutativo:  A . B  ≠  B . A

MATRIZ INVERSA

Dada una matriz cuadrada  A, si existe otra matriz  B  que verifique  A . B  =  B . A = I  (matriz identidad), entonces se dice que  B  es la matriz inversa de  A  y se representa por  A^-1.     ( A . A^-1 = A^-1 . A = I )

Si existe la matriz inversa  de  A, se dice que la matriz  A  es inversible o regular. En caso contrario, se dice que la matriz  A  es singular.

¿Cuándo tiene inversa una matriz? Una matriz  A  de orden  n  (n filas y n columnas) tiene inversa cuando su rango es  n, es decir, cuando el rango de dicha matriz coincide con su orden.

¿Cómo se puede calcular la inversa de una matriz? Básicamente hay tres procedimientos para calcular la inversa de una matriz. Son los siguientes:

1º Aplicando la definición y resolviendo los sistemas de ecuaciones correspondientes. Resulta muy laborioso cuando el orden de la matriz es superior a  2.

2º Por el método de Gauss.

3º Por determinantes y adjuntos

CALCULO DE LA INVERSA DE UNA MATRIZ POR EL MÉTODO DE GAUSS

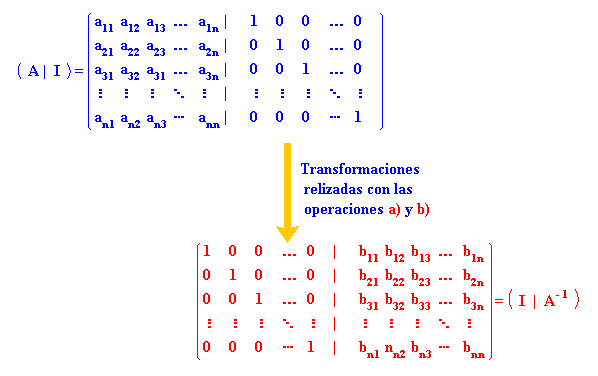
Para calcular la inversa de una matriz cuadrada  A, aplicando el método de Gauss, construimos, en primer lugar,  la matriz  ( A | I ), siendo  I  la matriz identidad del mismo orden que A. Después de realizar diversas operaciones sobre las filas de ésta  nueva matriz, tendremos que conseguir que se transforme en la siguiente  ( I | B ).  La matriz  B  será la inversa de la matriz  A,  es decir:  B = A^-1.

Las operaciones que podemos realizar con las filas de la citada matriz son:

a) Multiplicar o dividir una fila por un número distinto de cero.

b) Sumarle a una fila otra fila multiplicada por un número distinto de cero.