Metodo de Secante

Este método, a diferencia del de bisección y regla falsa, casi nunca falla ya que solo requiere de 2 puntos al principio, y después el mismo método se va retroalimentando.

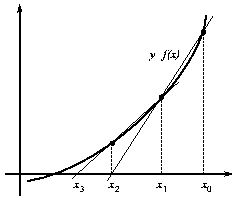
Lo que hace básicamente es ir tirando rectas secantes a la curva de la ecuación que se tiene originalmente, y va chequeando la intersección de esas rectas con el eje de las X para ver si es la raíz que se busca.

Procedimiento:

Primero hay que definir algunos conceptos como:

• Xn es el valor actual de X
• Xn-1 es el valor anterior de X
• Xn+1 es el valor siguiente de X

Para simplificar la formula que se usa en este método se dirá que:

• A=Xn-1
• B=Xn+1
• C=Xn

Como su nombre lo dice, este método va trazando rectas secantes a la curva original, y como después del primer paso no depende de otras cantidades sino que solito va usando las que ya se obtuvieron, casi nunca falla porque se va acomodando hasta que encuentra la raíz.

• Lo primero que se hace, igual que con otros métodos es dar 2 puntos cualesquiera que sean sobre el eje de las X que se llaman A y C.
• Después se sustituyen esos puntos en la ecuación original para obtener f(A) y f(C).
• Una vez que se tienen todos esos datos se obtiene el punto B con la formula B=((Af(C))-(C(f(A)))/(f(C)-f(A)).

A diferencia del resto de los métodos, aquí no hay que acomodar en columnas cada uno de los datos, sino que se utiliza la simplificación de conceptos y como se simplifica la formula para seguir con el método. Aqui solo se usan 2 columnas, una de Xn y otra de f(Xn).Vista previa

Algoritmo:

Entrada: Aproximación inicial de x0 y x1
Tolerancia T
Máximo número de iteraciones N
Salida: Un valor aproximado de la raíz o un mensaje de error

Paso1: Asigne i = 2
q0 = f(x0)
q1 = f(x1)

Paso2: Mientras i <= N0 haga Pasos 3-6

Paso3: Encuentre x = x1 - q1(x1 -x0) / (q1-q0)

Paso4: Si |x - x1 | < T

Entonces Salida (x);

Parar.

Paso5: Asigne i = i+1

Paso6: Asigne x0 = x1
x1 = x
q0 = q1
q1 = f(x)

Paso7: Salida ("Método falló luego de N0 iteraciones").

Parar