Metodo Gauss-Seidel

Para comenzar es preciso mencionar que es un método iterativo, es decir que debe aplicarse recursivamente hasta encontrar una solucion adecuada o con un error considerablemente pequeño.

En cada iteración obtenemos una solución posible del sistema con un error determinado, a medida que aplicamos nuevamente el método, la solución puede ser más precisa, entonces se dice que el sistema converge, pero si al aplicar el método reiteradas veces la solución tiene un error (ya explicaremos como se calcula este error) cada vez mayor se dice que el sistema no converge y no se puede resolver el sistema de ecuaciones por este método.

Bien proseguiré con la explicación del método y luego aclararé los detalles necesarios para determinar la eficacia del mismo.

Teniendo el siguiente sistema de ecuaciones:

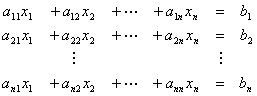
Despejamos x1 de la ecuación 1, x2 de la ecuación 2, … , xn de la ecuación n, quedando:

Desde la formula anterior resultan las fórmulas que se deberán ir aplicando en las diferentes iteraciones. Para comenzar a aplicar el método debemos asignar un valor arbitrario a las variables x2,…xn con el fin de obtener x1. Lo mas conveniente en este caso es que los valores comiencen en cero, lo cual nos facilitaría el trabajo ya que se reduce el cálculo de las primeras soluciones, entonces de esto resulta que:

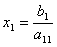
Ahora despejamos x2 de la ecuación 2 y reemplazamos a x1 por el valor obtenido en la ecuación anterior. De esto nos queda:

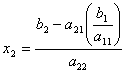
Una vez que tenemos x2, despejamos x3 de la ecuación 3 y así sucesivamente con las n ecuaciones, cada vez asignando el valor de las x1, x2, … xn-1 obtenido en el paso anterior.

Cuando hemos despejado las xn, tenemos lo que se conoce como primera solución o solución de la primer iteración:

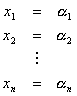
Con los nuevos valores de x1, x2,…,xn aplicamos los mismos pasos anteriores pero con los nuevos valores de las xn, de esta manera conseguimos una segunda solución:

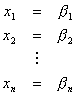
Al tener esta segunda solución estamos en condiciones de calcular el error que se calcula como sigue:

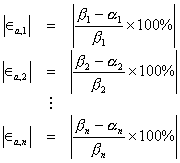
Así, repetimos el método tantas veces hasta que el error sea muy pequeño o los suficientemente aceptable.

Ahora solo queda mencionar que para que un sistema sea convergente se debe cumplir que la matriz de coeficientes sea diagonalmente dominante, y para ello se debe verificar la siguiente expresión:

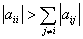
Si no se cumple esa condición, se puede permutar las filas de la matriz, con el fin de poder convertirla en una diagonalmente dominante.