Metodo de la Regla Falsa

En cálculo numérico, el método de regula falsi (regla falsa) o falsa posición esun método iterativo de resolución numérica de ecuaciones no lineales. El método combina el método de bisección y el método de la secante.

Este método sirve para encontrar la raíz o solución real de una ecuación. Al decir que encuentra su resultado hay que tomar en cuenta que no todas las ecuaciones tienen un solo resultado, y que no todas tienen resultado, por lo que hay que tener una idea dela forma de la curva de la ecuación antes de aplicar el método para que sea efectivo.

PROCEDIMIENTO

Como mencionamos anteriormente, sería bueno considerar si la raíz de una ecuación está localizada más cerca de alguno de los extremos del intervalo.

• Consiste en considerar un intervalo (xi, xs) en el que se garantice que la función tiene raíz. 
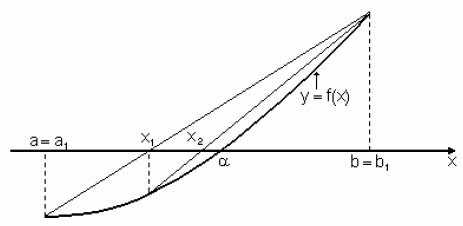
• Se traza una recta que une los puntos (xi, f(xi)), (xs, f(xs)) 
• Se obtiene el punto de intersección de esta recta con el eje de las abscisas: (xr, 0); se toma xr como aproximación de la raíz buscada. 
• Se identifica luego en cuál de los dos intervalos está la raíz. 
• El proceso se repite n veces, hasta que el punto de intersección xr coincide prácticamente con el valor exacto de la raíz. 

Método de la regla falsa - Aplicación en Matlab:

disp(' METODO DE LA REGLA FALSA ');
disp(' ---------------------- ');

%f=input('INGRESE FUNCION: ','s');
f='exp(-x)-log(x)';
%xai=input('INGRESE LIMITE INFERIOR DEL INTERVALO: ');
xai=1;
%xbi=input('INGRESE LIMITE SUPERIOR DEL INTERVALO: ');
xbi=2;


%tol=input('INGRESE PORCENTAJE DE ERROR: ');
tol=1;


f=inline(f);
i=1;
ea(1)=100;

if f(xai)*f(xbi) <>= tol,
if f(xa(i))*f(xr(i))<> 0
xa(i+1)=xr(i);
xb(i+1)=xb(i);

end


%xr(i+1)=(xa(i+1)+xb(i+1))/2;
xr(i+1)=xa(i+1)-(f(xa(i+1))*(xb(i+1)-xa(i+1)))/(f(xb(i+1))-f(xa(i+1)));
ea(i+1)=abs((xr(i+1)-xr(i))/(xr(i+1))*100);
fprintf('%2d \t %11.7f \t %11.7f \t %11.7f \t %7.3f \n',...
i+1,xa(i+1),xr(i+1),xb(i+1),ea(i+1));
i=i+1;
end

else

fprintf('No existe una raíz en ese intervalo');

end